During partial pivoting Guassian elimination (PPGE) of a matrix (just like regular GE, except we choose as a pivot the element which satisfies \({\max}_i|a_{ij}|\) for each column \(A^{(j)}\)), one sometimes accumulates large intermediate values——so much so that the final result in unreachable because of overflow. The following is a classical example: \[ A = \begin{bmatrix} 1 & 0 & 0 & 0 & 1\\ -1 & 1 & 0 & 0 & 1\\ -1 & -1 & 1 & 0 & 1\\ -1 & -1 & -1 & 1 & 1\\ -1 & -1 & -1 & -1 & 1\\ \end{bmatrix} \to \begin{bmatrix} 1 & 0 & 0 & 0 & 1\\ 0 & 1 & 0 & 0 & 2\\ 0 & 0 & 1 & 0 & 4\\ 0 & 0 & 0 & 1 & 8\\ 0 & 0 & 0 & 0 & 16\\ \end{bmatrix} = B \] For a \(n\) by \(n\) matrix as formulated above, PPGE will result in a matrices whose maximal element is \(\leq 2^{n-1}\). In fact, this is the worst case scenario. For much larger matrices, say $1000 \times 1000$, we are going to run into problems. Despite this, PPGE is by far the most popular method for accomplishing LU decomposition, and system solving. Why? Basically, the catastrophic example above is possible, but unrealistic.
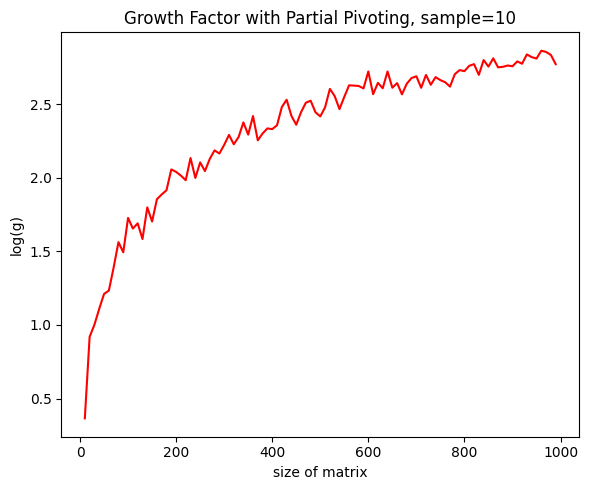
One calls the ratio of the maximal elements in absolute value of \(A\) and \(B\) the "growth factor" of \(A\), or \(g(A)\). As one would expect, the larger the matrix \(A\), the larger its growth factor (in the example above, this relationship is \(2^{n-1}\)):
This data is derived from normally distributed real matrices. Surprisingly, we don't see as exaggerated growth factors as the contrived example let on, and even the $\approx1000\times1000$ matrices are well suited for computation with PPGE. Hence: how likely is it that we run into examples remotely as bad as the initial example? We plot to find out that the answer is "almost never":
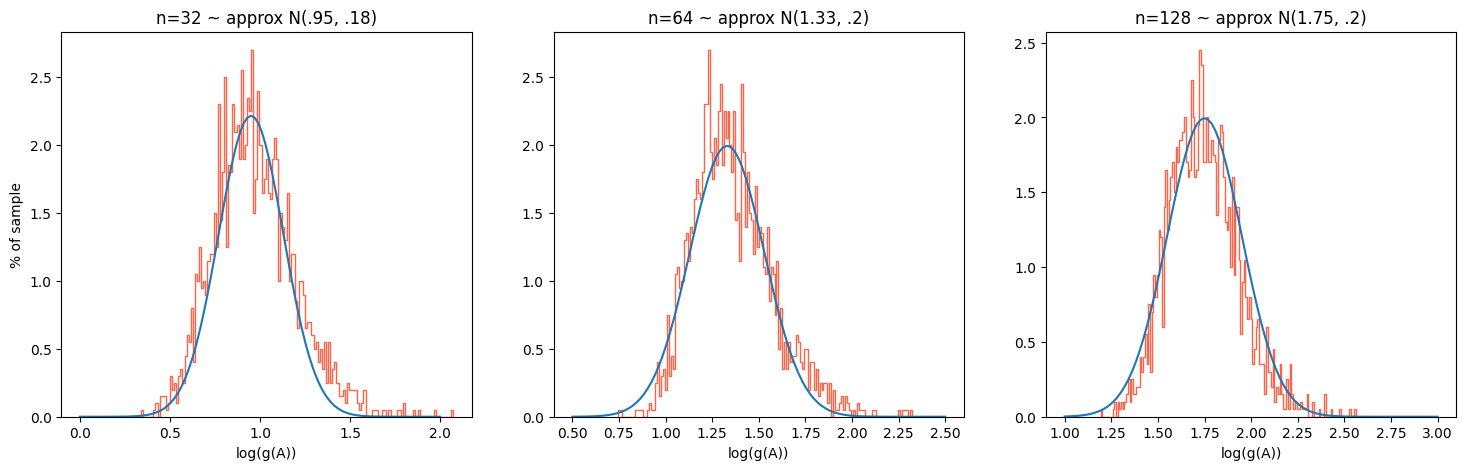
The above analysis only involves a few hundred sample matrices of each size. A sample of 5000 16x16 matrices yields similar behavior:
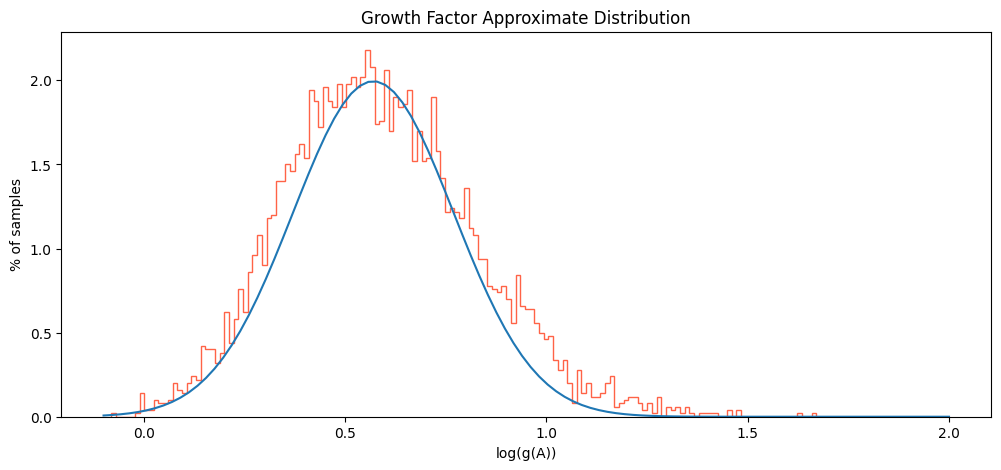
Which is to say, with growth factors that cap out at \(e^{1.7} \approx 5.5\), we are not ever getting close to the foretold bound of \(g(A) \leq 2^{16 }\approx 65,000\)
A Bézier curve interpolates between some data in \(\mathbb{R}^n\), usually points on a plane (one can shift control points to fit a desired shape, and it isn't too hard to succeed this way). Kaur and Goyal recently developed an "\(\alpha\)-Bézier," where, the larger the parameter \(\alpha \in \mathbb{R}\) is, the closer the Bézier interpolation will hug our control points. Conversely, a sufficiently low \(\alpha\) parameter will make the control polygon repel the Bézier. So, given some points in \(\mathbb{R}^2\), we could observe increasingly strict interpolations, say through animation, including that of a standard Bézer (\(\alpha=1\)).
A Bézier curve typically maps the unit interval onto a curve in \(\mathbb{R}^n\). One can generate a "curve of curves" to map the unit square onto a surface. This is called a tensor product surface, or Bézier surface, in the case of ordinary Bézier curves. Hence, we apply the ideas above, generating increasingly strict interpolations of roughly paraboloidic control data via \(\alpha\)-Bézier tensor surface patches. The result is disconcerting, but cool (\(-1 \leq\alpha\leq 3\)). If one spends enough time designing a control grid, one may be able to use this method to generate the world's most computationally inefficient animation of a beating heart. The math: \[ \{ T(t, s) \}_{\alpha \in (-1, 3)} = \left\{\sum{_{i=0}^{3}}\sum{_{j=0}^{3}}B_i^n(t, \alpha)B_j^m(s, \alpha)\vec{v_{ij}} : \alpha \in (-1, 3) \right\} \leftarrow \text{ tensor surface computation}\] \[\text{where } B_i^n := \left[\binom{n-2}{i}(1-\alpha)t + \binom{n-2}{i-2}(1-\alpha)(1-t) +\binom{n}{i} \alpha t(1-t)\right]t^{i-1}(1-t)^{n-i-1} \leftarrow \text{ alpha-Bezier}\]
You are tying to find your soulmate, and thankfully \(N\) people have lined up for a "date." You don't know who exactly is the best candidate among them, but you can conduct interviews, one by one, to gather information. You can only interview a person once, and you must decide to choose them, or not, after the interview concludes. What strategy should you use to optimize the probability that, supposing your soulmate is in line, you pick him/her? The answer to this (preliminary) question is odd: you interview and reject \(k\) candidates, and then pick the first \((k+i)^{th}\) candidate who is better than all those previous. If \(k\) is picked ideally, the odds of choosing your soulmate are approximately \(1/e\), and what's more, the ideal ratio of \({k}/{N}\) is also \({1}/{e}\)! Here is the logic: \[ \begin{array}{rl} \mathbb{P}(\text{Soulmate chosen}) =& \; \mathbb{P}(\text{Soulmate chosen in \(k+1^{th}\) interview})\\ +& \; \mathbb{P}(\text{Soulmate chosen in \(k+2^{nd}\) interview})\\ \vdots&\\ +& \; \mathbb{P}(\text{Soulmate chosen in ${N}^{th}$ interview})\\ =& \sum_{i=1}^{N-k} \mathbb{P}(\text{Soulmate chosen in $(k+i)^{th}$ interview}) \end{array} \] Applying Bayes': \[\sum_{i=1}^{N-k}\mathbb{P}(S \text{ chosen @ } i) = \sum_{i=1}^{N-k}\mathbb{P}(\text{Given that }S_i = S, \; S_i \text{ chosen})\mathbb{P}(S_i = S)\] where \(S_i\) is the \(i^{th}\) person interviewed after the initial round of rejects, and \(S\) is your soulmate. Immediately, we see that the probability of any candidate being your soulmate, \(\mathbb{P}(S_i = S)\), is \({1}/{N}\). If \(S_i\) is given to be "the one," they are chosen only if the best candidate thus far was preliminarily rejected (otherwise, he/she would have been selected, not \(S_i\)). Thus, we have \(\mathbb{P}(S_i\text{ chosen | }S_i = S) = {k}/{(k+i-1)}\). \[\mathbb{P}(S \text{ is chosen}) = \sum_{i=1}^{N-k}\mathbb{P}(S \text{ chosen in interview } i) = \sum_{i=1}^{N-k}\frac{k}{N(k+i-1)}\] One can express this summation, using some calculus, as an approximation of a Riemann integral, as follows: \[m \int_{m}^{1}\frac{1}{x}dx = m\ln(x)\left|_{m}^{1}\right. = -m\ln(m)\] where \(m\) is the limiting case of \({k}/{N}\). When this expression is maximized by differentiating and setting to 0, one yields \({k}/{N} = {1}/{e} \), and thus the probability of picking your soulmate with the above-defined ratio is also \({1}/{e}\). That's 37%!
Some years ago I recorded a sample library of the piano pictured below, comprised of each note played at 4 volumes, in 4 audio channels. Recently, I put together VST and AU plugins using the JUCE C++ framework, which maps each MIDI channel (corresponding to the acoustic piano layout) to a group of samples, which are chosen based on the strength at which the note was triggered. You can take it for a spin yourself, or check out some "recordings" of jazz classics below, made with MIDI from Doug McKenzie.
